Industrial Ring and Wheel Rolling Simulations

Industrial ring-rolling processes have been used widely since the 19th Century to produce seamless wheels and rings for bearings, railway tires, and other types of seamless, ring-shaped components for aerospace, automotive, petroleum, mechanical and nuclear industries. According to basic principles the ring rolling process may be classified into two main groups, i.e. radial rolling and radial-axial rolling.

The deformation is based on squeezing the ring in a radial direction by decreasing the gap between a main roll and mandrel. Guide and axial rolls are important, too: Guide rolls control the circularity and axial rolls control the ring height during the process.^[1] 

For successful ring rolling in mass production there is a need to estimate the required forces and torques, understanding the metal flow, and how to get the exact final product shape, avoiding cracks, laps and other defects. Both experimental and simulation approaches can be used to find the best working parameters. Simulation is much less expensive than industrial experimentation, as well as easier and faster. It offers accuracy and helps to set process parameters and optimal settings for a rolling machine. Also, it provides optimal product quality, saves energy and material, and helps to avoid accidents due to overloading.

Cost-reduction strategies increasingly require production of rings with complex cross-sectional shape to be closer to the final shape. This kind of profiled ring is more difficult to roll, and the use of numerical modelling becomes vital.

Ring and wheel rolling usually are classified as incremental bulk-forming processes. However, the advantages are directly related to the complexities in the process design, in particular, the very limited contact area where the deforming load is applied makes it difficult to control the metal flow. The cyclic (non-monotonic) character of loading, along with localized load application develop significant residual stresses, which can lead to fracturing of the part.

The high cost of trials, the large number of control parameters, and the wide range of possible failures make the “trial and error” approach costly and inefficient. Thus, robust and reliable simulation methods are critical for effective implementation and development of ring-rolling processes.

Simulation approach —  The specific needs of ring-rolling process simulation prompted the development of a dual-mesh method that also has been implemented to some other metal forming processes with highly localized deformation, such as cogging, rolling etc. Originally, the two-mesh approach was proposed^[2] for ring-rolling simulation to reduce the computational time, and to minimize the volume variation in simulations. They implemented prismatic (brick) elements that were difficult to remesh, so these types of elements were difficult to implement for simulation of profiled rings and flanges due to the high concentration of plastic deformation. We implemented a dual mesh approach that is based on tetrahedral finite elements, which are more suitable for automatic remeshing.^[3,4]

We have implemented for simulation two different FE meshes that can be called “computational” and “geometrical” (see Fig.1.)

The “computational” mesh is used to solve the mechanical problem. It is highly variable in size and it is very fine in zones of deformation, while quite coarse in “rigid” zones outside of the contact with the rolls.

The rolls themselves also have very fine mesh at the area of contact with the ring, to provide precise approximation of the friction and heat-transfer conditions.

The “computational” mesh achieves precise prediction of the strain-rate distribution. The “geometrical” mesh is more regular but all the elements have very small size. It accurately records the “history” of deformation (the deformed shape of the ring and the strain distribution it.)

Also, this mesh provides precise simulation of the thermal problem using dense distributed nodes, as Voronoi noted^[4]. When considering the ring-rolling process we usually simulate a complete technological chain that includes forging operations (billet upsetting, closed-die forging, piercing), then actual ring rolling, and then heat treatment.

Setting up the ring-rolling simulation — The model for ring-rolling simulation includes the following objects:
•  Rolled ring (workpiece);
•  Main roll;
•  Mandrel;
•  Axial rolls for dual stand mill;
•  Guide rolls.

Each roll has its own axis to be specified. The guide rolls also have a second axis that are actually pivot points of the centering mechanism. Figure 2 shows the computational model setup, including a ring and all rolls with indication of their possible movement directions for typical double stand rolling machine.

The ring-rolling simulation requires the same source data to be specified as for an actual ring-rolling machine, such as:
•  Main roll speed of rotation, rpm;
•  The final diameter of the ring;
•  Load applied by the centering rolls;
•  Ring growth speed (RGS);
•  Dependence of the ring height on its thickness (lamination curve);
•  Diameters and configuration of all rolls.

The main roll has a rotation due to motor drive while the mandrel is free rotating and zero torque is supposed to be specified as a boundary condition. Radial movement of the mandrel and vertical movement of the axial rolls can be specified two ways in the program. In the first way, we specify Ring Growth Speed (RGS) and lamination curve, as shown in the Figure 3a.

In this case the program automatically calculates the radial movement of the mandrel and vertical movement of the axial rolls. By means of a lamination curve the user specifies the dependence of the thickness on the height of the ring and the desired RGS. This approach provides good results, mostly for the rings with rectangular cross sections.

For shaped rings, it is necessary to tune the process parameters. In this case, the simulation helps to adjust the RGS and lamination curve to get the desired ring dimension and shape by means of computational trials, saving time and material. Fig. 3b shows another method of source data specification for a ring rolling process when the position of the mandrel and both cones are directly specified by the velocity graphs as follows:
•  Radial velocity of the mandrel versus time;
•  Axial velocity of the cones versus time.

Cones (axial rolls) may move in horizontal and vertical directions. The horizontal movement may be dependent on the ring diameter. Guide rolls support the ring and control its position. The load applied to guide rolls may be dependent on the ring diameter. Mandrel radial velocity also may be variable and dependent on the load that, in turn, is controlled by a hydraulic drive applied in radial direction to the mandrel.

In general, all process parameters are equally vital for industrial implementation of simulation because they may influence the shape of the ring, temperature, and strain distribution in its cross-sectional area. The simulation also provides information about the temperature and stress distribution in the rolls, as shown in the Figure 4.

Predicting material flow defects in a ring-rolling process is a difficult task that can be achieved by implementing the developed model. Figure 5 shows the lap defect that appears on the bottom surface of the ring while the ring lateral surface becomes conical.

These simulation results are in good agreement with practical observations. To fix these defects, a new preform shape has been developed and then tested by means of numerical trials. Finally, it provided a flat bottom and straight cylindrical surface for the ring.

Another typical ring rolling defect is underfilling of the roll cavity, as shown in Figure 6 (by courtesy of Caltek Ltd., South Korea.)

This technology and the machine to produce it was developed by the company Caltek (www.caltek.co.kr.) In the example shown, the material was AISI 1020 carbon steel, the speed of the main roll was 30 rpm, and the initial workpiece temperature was 1,230°C. The movement of the mandrel and axial rolls are specified using velocity graphs. As seen from Fig. 6b, the simulation predicted the shape of the ring very close to reality. Modification of the preform shape developed by computer trials finally helped to avoid this kind of the defect and produce a good quality ring.

Another way to improve ring rolling by simulation is predicting grain size and mechanical properties of a seamless ring made of alloyed material. Figure 7 shows ring rolling of Inconel 718. The full technological chain consists of six intermediated cycles of heating and cooling for the billet, seven forging operations, and one ring rolling operation. In this process, ring rolling is an intermediate step between the forging sequence and heat treatment. Figure 7 shows the predicted distribution of the grain size inside the ring according to ASTM standard. The subroutine for microstructure simulation is included in the QFormRR package, and predicts grain size at tracked points of the investigated workpiece. The subroutine is developed in collaboration with GMT Berlin^[5].

Verifying results of ring-rolling simulation — Verification of ring-rolling simulations have been done using several industrial case studies. In the first case, we have verified the predicted mandrel and axial rolls forces in a SMS Meer RAW 500-400 double stand machine by comparing them with experimental results from work^[6] as depicted in Figure 8.

The initial ring, from a rectangular cross-section made of AISI 4140 steel, weighs 1,350 kg. The motion of the mandrel and axial rolls versus time during the process have been specified using parameters from work^[6]. As shown, the graphs of radial and axial forces measured experimentally and obtained in simulation are in good agreement.

In the next study, we investigated the radial ring-rolling process without applying cone rolls and leaving the upper and lower ring surfaces to deform freely. The results of the experiment have shown a fishtail shape on the surface of the rolled ring. The study was done in collaboration with Schmiedewerke Gröditz GmbH (and included here by courtesy of Eng. Alexander Kovalev.)

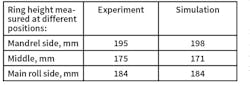
Prior to rolling the ring had these dimensions: diameter, 670 mm; width, 195 mm; and height, 160 mm. The real shape of the ring after rolling is shown in Figure 9a. The dimensions of the ring obtained in simulation are shown in Figures 9b and c. Both experiment and simulation have shown the nonsymmetrical fishtail formation. The heights at different positions are presented in Table 1. The difference between experimental and simulated height values is not more than 5%, proving that simulations are effectively accurate for practical purposes.